122. 买卖股票的最佳时机 II

Similar Question

714. 买卖股票的最佳时机含手续费 - 力扣（LeetCode）

就只是卖出的时候多减一个手续费就可以了

Solution Tips

方案一: 峰谷法

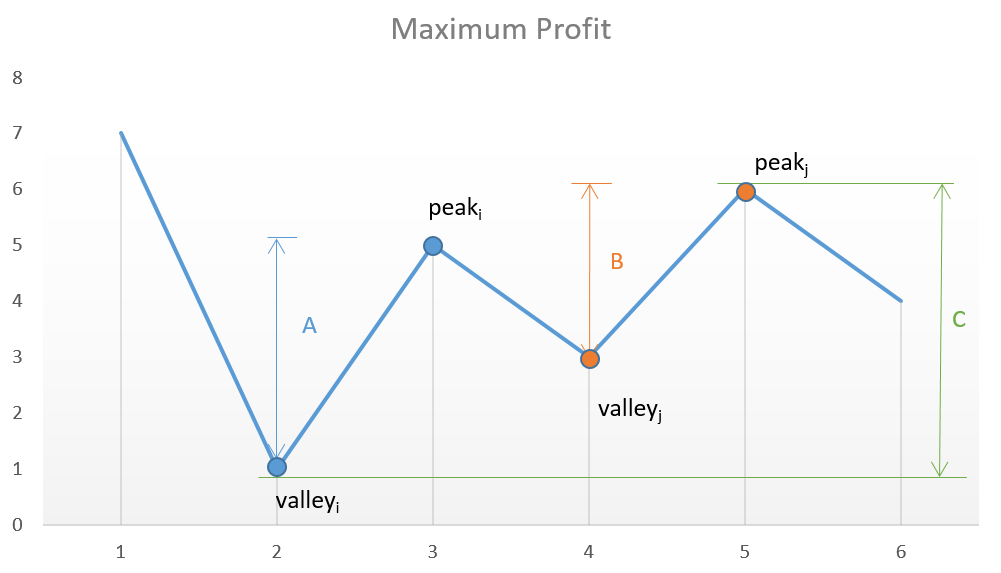
如果我们分析图表，那么我们的兴趣点是连续的峰和谷。

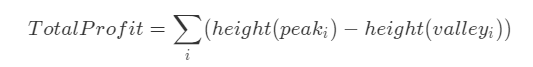
关键是我们需要考虑到紧跟谷的每一个峰值以最大化利润。如果我们试图跳过其中一个峰值来获取更多利润，那么我们最终将失去其中一笔交易中获得的利润，从而导致总利润的降低。

试图通过考虑差异较大的点以获取更多的利润，获得的净利润总是会小与包含它们而获得的静利润，因为 C 总是小于 A+B。

  var maxProfit = function(prices) {
    const len = prices.length
    if(len==0) return 0
    let profit = 0
    let valley = 0 , peak = 0
    let i = 0
    while(i<len-1){
      while(i<len-1&&prices[i]>prices[i+1]) i++
      // 跳出内循环，遇到谷了
      valley = prices[i]
      while(i<len-1&&prices[i]<=prices[i+1]) i++
      // 跳出内循环，遇到峰
      peak = prices[i]
      // 找到了一对 谷 峰
      profit += peak - valley
    }
    return profit
  };

复杂度分析

• 时间复杂度：O(n)。遍历一次。
• 空间复杂度：O(1)。需要常量的空间。

方案二: 贪心算法

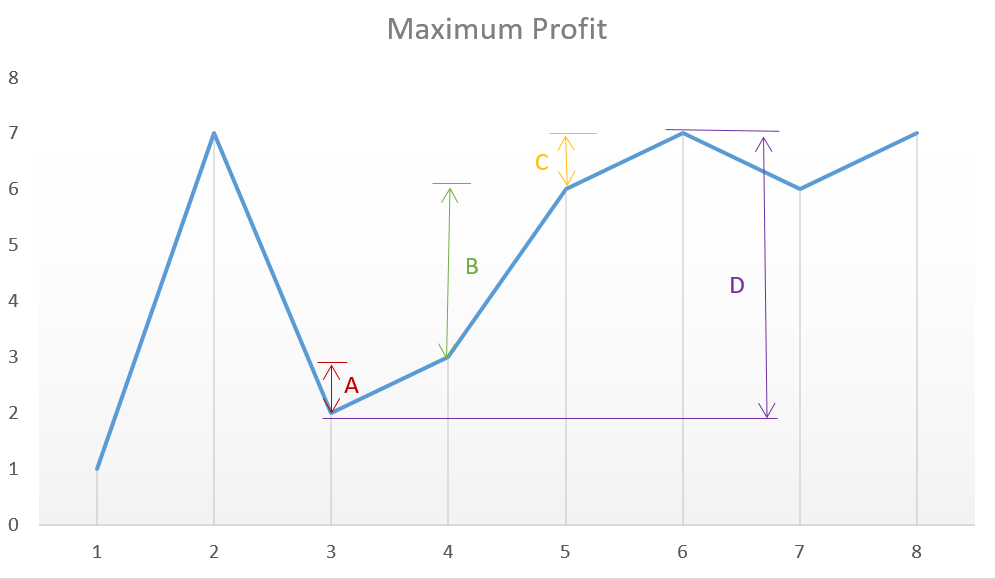
该解决方案遵循 方法一 的本身使用的逻辑，但有一些轻微的变化。在这种情况下，我们可以简单地继续在斜坡上爬升并持续增加从连续交易中获得的利润，而不是在谷之后寻找每个峰值。最后，我们将有效地使用峰值和谷值，但我们不需要跟踪峰值和谷值对应的成本以及最大利润，但我们可以直接继续增加加数组的连续数字之间的差值，如果第二个数字大于第一个数字，我们获得的总和将是最大利润。这种方法将简化解决方案。 这个例子可以更清楚地展现上述情况：

[1, 7, 2, 3, 6, 7, 6, 7]

从上图中，我们可以观察到 A+B+C 的和等于差值 D 所对应的连续峰和谷的高度之差。

  var maxProfit = function(prices) {
    const len = prices.length
    if(len==0) return 0
    let profit = 0
    for (let i = 0; i < len-1; i++) {
      if(prices[i]<prices[i+1]){
        profit += prices[i+1]-prices[i]
      }
    }
    return profit
  };

方案三: 动态规划

跟贪心算法差不多，定义最大利润为 dp[i] 对应的状态

只要价格上升，利润就会上升，

  var maxProfit = function(prices) {
    const len = prices.length
    if(len==0) return 0
    let dp=[]
    dp[-1] = 0
    for (let i = 0; i < len-1; i++) {
      if(prices[i]<prices[i+1]){
        dp[i] = dp[i-1] + prices[i+1] - prices[i]
      }else{
        dp[i] = dp[i-1]
      }
    }
    return dp[len-2]
  };

本质：是找到所有的上升子序列

本质上也是对着贪心做动态规划.

方案四: 股票问题通用 Dp

var maxProfit = function(prices) {
    const n = prices.length;
    const dp = new Array(n).fill(0).map(v => new Array(2).fill(0));
    dp[0][0] = 0, dp[0][1] = -prices[0];
    for (let i = 1; i < n; ++i) {
        dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
        dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
    }
    return dp[n - 1][0];
};

滚动数组优化

var maxProfit = function(prices) {
    const n = prices.length;
    let dp0 = 0, dp1 = -prices[0];
    for (let i = 1; i < n; ++i) {
        let newDp0 = Math.max(dp0, dp1 + prices[i]);
        let newDp1 = Math.max(dp1, dp0 - prices[i]);
        dp0 = newDp0;
        dp1 = newDp1;
    }
    return dp0;
};